Exploring Google's ortools - Part 1

Introduction to linear programming and optimization with ortools.

Introduction

I recently came across Google's ortools library and I was immediately curious to explore it. I wanted to give it a try against some of the optimization problems I used to solve using a combination of Excel's Solver¹ and the Simplex method² some years ago. I decided to start with a simple linear programming problem and see how it goes.

The problem comes from exercise 3.3 of Linear Programming and Network Flows³.

Consider the following problem:

\[ \begin{align} \text{Maximize} \quad x_1 + 3 x_2\\ \text{subject to} \quad x_1 - 2 x_2 &\leq 0 \\ -2 x_1 + x_2 &\leq 4 \\ 5 x_1 + 3 x_2 &\leq 15 \\ x_1, x_2 &\geq 0 \end{align} \]

Solve this problem graphically.

Solve the problem by the simplex method.

Solution

Graphical Solution

The graphical solution is straightforward. We plot the constraints and find the feasible region. Then we plot the objective function and find the optimal solution.

ex3_3_graphical_solution.py

# /// script
# dependencies = [
#   "matplotlib",
#   "numpy",
# ]
# ///

import os
from functools import reduce
from operator import and_

import matplotlib.pyplot as plt
import numpy as np

d = np.linspace(0, 10, 300)
x, y = np.meshgrid(d, d)

# Create conditions for the feasible region
conditions = (
    (x >= 0),
    (y >= 0),
    (x - 2 * y <= 0),
    (-2 * x + y <= 4),
    (5 * x + 3 * y <= 15),
)

# Plot the feasible region
plt.imshow(
    reduce(and_, conditions),  # apply & operator to all conditions
    extent=(x.min(), x.max(), y.min(), y.max()),
    origin="lower",
    cmap="Greys",
    alpha=0.3,
)

# Plot the constraints
x = np.linspace(0, 16, 2000)
c1_y = x / 2
c2_y = 4 + 2 * x
c3_y = (15 - 5 * x) / 3

plt.plot(x, c1_y, label=r"$x_2 \geq x_1/2$")
plt.plot(x, c2_y, label=r"$x_2 \leq 4 + 2x_1$")
plt.plot(x, c3_y, label=r"$x_2 \leq 5 - 5x_1/3$")
plt.xlim(0, 10)
plt.ylim(0, 10)

plt.legend()
plt.savefig(
    os.path.join(
        __file__,
        "../../../posts/img/ortools/ex3_3_graphical_solution.png",
    )
)

Output

The feasible region is the shaded area in the plot below.

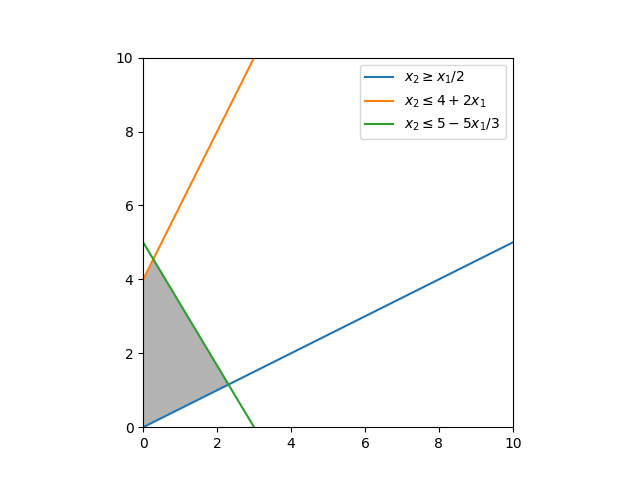
Graphical solution of the linear programming problem

Analysis

From the plot, we can see that the optimal solution is at the intersection of the lines \(x_2 = 4 + 2x_1\) and \(x_2 = 5 - 5x_1/3\). The optimal solution is at \(x_1 = \frac{3}{11}\) and \(x_2 = \frac{50}{11}\), and the optimal value of the objective function is \(\frac{153}{11} \approx 13.91\).

Solution with ortools

Now, let's solve the same problem using ortools.

ex3_3_ortools_solution.py

# /// script
# dependencies = [
#   "ortools",
# ]
# ///

"""Solve exercise 3.3 from the book.

Maximize      X1 + 3X2
subject to    X1 - 2X2 <= 0
            -2X1 +  X2 <= 4
             5X1 + 3X2 <= 15
              X1,   X2 >= 0.
"""

import sys

from ortools.linear_solver import pywraplp

# Create the linear solver with the GLOP backend
solver = pywraplp.Solver.CreateSolver("GLOP")
if not solver:
    print("The solver could not be created.")
    sys.exit(1)

# Create the variables x and y.
x1 = solver.NumVar(0, solver.infinity(), "x1")
x2 = solver.NumVar(0, solver.infinity(), "x2")
print("Number of variables =", solver.NumVariables())

# Create a linear constraint, X1 - 2X2 <= 0.
ct = solver.Constraint(-solver.infinity(), 0, "ct0")
ct.SetCoefficient(x1, 1)
ct.SetCoefficient(x2, -2)

# Create a linear constraint, -2X1 + X2 <= 4.
ct = solver.Constraint(-solver.infinity(), 4, "ct1")
ct.SetCoefficient(x1, -2)
ct.SetCoefficient(x2, 1)

# Create a linear constraint, 5X1 + 3X2 <= 15.
ct = solver.Constraint(-solver.infinity(), 15, "ct2")
ct.SetCoefficient(x1, 5)
ct.SetCoefficient(x2, 3)

print("Number of constraints =", solver.NumConstraints())

# Create the objective function, X1 + 3X2.
objective = solver.Objective()
objective.SetCoefficient(x1, 1)
objective.SetCoefficient(x2, 3)
objective.SetMaximization()

print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL:
    print("Solution:")
    print("Objective value =", objective.Value())
    print("X1 =", x1.solution_value())
    print("X2 =", x2.solution_value())
else:
    print("The problem does not have an optimal solution.")

print("\nAdvanced usage:")
print(f"Problem solved in {solver.wall_time():d} milliseconds")
print(f"Problem solved in {solver.iterations():d} iterations")

Output

The output of the script is:

Number of variables = 2
Number of constraints = 3
Solving with Glop solver v9.10.4067
Solution:
Objective value = 13.909090909090907
X1 = 0.2727272727272725
X2 = 4.545454545454545

Advanced usage:
Problem solved in 0 milliseconds
Problem solved in 2 iterations

Conclusion

As you can see, ortools reached the same optimal solution as the graphical solution. The library is easy to use and provides a simple interface to solve optimization problems.

In this blog post we explored a simple linear programming problem, but ortools can also solve other types of optimization problems, including:

Constraint optimization
Mixed-integer optimization
Assignment
Scheduling
Packing
Routing
Network flows

In the next post, we will explore a different type of optimization problem using ortools.

Appendix: environment

The scripts are executed with uv and PEP 723.

$ uv run docs/snippets/operations-research-1/ex3_3_graphical_solution.py
Reading inline script metadata from: docs/snippets/operations-research-1/ex3_3_graphical_solution.py

$ uv run docs/snippets/operations-research-1/ex3_3_ortools_solution.py > docs/snippets/operations-research-1/ex3_3_ortools_solution_output.txt
Reading inline script metadata from: docs/snippets/operations-research-1/ex3_3_ortools_solution.py

Solver is a Microsoft Excel add-in program you can use to find an optimal value for the formula in a cell. ↩
The Simplex method is a popular algorithm for solving linear programming problems. ↩
Mokhtar S. Bazaraa, John J. Jarvis, Hanif D. Sherali, Linear Programming and Network Flows, 4th Edition, Wiley, 2010. ↩